《 具体数学:计算机科学基础(第二版) 》第一章的“约瑟夫问题”中,介绍了一种求解递归式的奇妙技巧 —— Repertoire Method 。这种技巧帮助我们将特殊解推向一般解:通过一些已知其解的参数函数,从特殊的情形推向一般的情形。
求解约瑟夫问题
以约瑟夫问题为例子,书中给出了如下的递推式:
J ( 1 ) = 1 J ( 2 n ) = 2 J ( n ) − 1 ( n ⩾ 1 ) J ( 2 n + 1 ) = 2 J ( n ) + 1 ( n ⩾ 1 )
\begin{equation}
\begin{array}{rll}
J(1) & = 1 & \\
J(2n) & = 2J(n) - 1 & (n \geqslant 1) \\
J(2n + 1) & = 2J(n) + 1 & (n \geqslant 1) \\
\end{array}
\end{equation}
J ( 1 ) J ( 2 n ) J ( 2 n + 1 ) = 1 = 2 J ( n ) − 1 = 2 J ( n ) + 1 ( n ⩾ 1 ) ( n ⩾ 1 )
列举已知解
我们按照递归式 ( 1 ) (1) ( 1 )
观察与推测
从上述表格可以看到,J ( n ) J(n) J ( n ) 2 2 2 J ( n ) = 1 J(n) = 1 J ( n ) = 1 J ( 2 m ) = 1 , m ⩾ 0 J(2^{m}) = 1,m \geqslant 0 J ( 2 m ) = 1 , m ⩾ 0 2 2 2 n n n n = 2 m + l n = 2^{m} + l n = 2 m + l 2 m 2^{m} 2 m n n n 2 2 2 l l l 2 m 2^{m} 2 m l = n − 2 m l = n - 2^{m} l = n − 2 m
因此,我们可以推断递归式 ( 1 ) (1) ( 1 )
J ( 2 m + l ) = 2 l + 1 ( m ⩾ 0 , 0 ⩽ l < 2 m )
\begin{equation}
\begin{array}{lll}
J(2^{m} + l) & = 2l + 1 & (m \geqslant 0, 0 \leqslant l < 2^{m}) \\
\end{array}
\end{equation}
J ( 2 m + l ) = 2 l + 1 ( m ⩾ 0 , 0 ⩽ l < 2 m )
现在我们对 m m m ( 2 ) (2) ( 2 )
∵ \because ∵ m = 0 m = 0 m = 0 l = 0 l = 0 l = 0 ∴ \therefore ∴ J ( 2 0 + 0 ) = 2 × 0 + 1 = 1 J(2^{0} + 0) = 2 \times 0 + 1 = 1 J ( 2 0 + 0 ) = 2 × 0 + 1 = 1
∵ \because ∵ m > 0 m > 0 m > 0 2 m + l = 2 n 2^{m} + l = 2n 2 m + l = 2 n l l l ∵ \because ∵ ( 1 ) (1) ( 1 ) J ( 2 n ) = 2 J ( n ) − 1 J(2n) = 2J(n) - 1 J ( 2 n ) = 2 J ( n ) − 1 ( 2 ) (2) ( 2 ) J ( 2 m + l ) = 2 l + 1 J(2^{m} + l) = 2l + 1 J ( 2 m + l ) = 2 l + 1
∴ J ( 2 m + l ) = 2 J ( 2 m − 1 + l / 2 ) − 1 = 2 × ( 2 × l / 2 + 1 ) − 1 = 2 l + 1
\begin{array}{rl}
\therefore J(2^{m} + l) & = 2J(2^{m - 1} + l / 2) - 1 \\
& = 2 \times (2 \times l / 2 + 1) - 1 \\
& = 2l + 1
\end{array}
∴ J ( 2 m + l ) = 2 J ( 2 m − 1 + l /2 ) − 1 = 2 × ( 2 × l /2 + 1 ) − 1 = 2 l + 1 同理,∵ \because ∵ m > 0 m > 0 m > 0 2 m + l = 2 n + 1 2^{m} + l = 2n + 1 2 m + l = 2 n + 1 l l l ∵ \because ∵ ( 1 ) (1) ( 1 ) J ( 2 n + 1 ) = 2 J ( n ) + 1 J(2n + 1) = 2J(n) + 1 J ( 2 n + 1 ) = 2 J ( n ) + 1
∴ J ( 2 m + l ) = 2 J ( 2 m − 1 + ( l − 1 ) / 2 ) + 1 = 2 × ( 2 × ( l − 1 ) / 2 + 1 ) + 1 = 2 l + 1
\begin{array}{rl}
\therefore J(2^{m} + l) & = 2J(2^{m - 1} + (l - 1) / 2) + 1 \\
& = 2 \times (2 \times (l - 1) / 2 + 1) + 1 \\
& = 2l + 1
\end{array}
∴ J ( 2 m + l ) = 2 J ( 2 m − 1 + ( l − 1 ) /2 ) + 1 = 2 × ( 2 × ( l − 1 ) /2 + 1 ) + 1 = 2 l + 1 综上可证,式子 ( 2 ) (2) ( 2 )
推广:引入通用参数
通过引入常数 α \alpha α β \beta β γ \gamma γ ( 1 ) (1) ( 1 ) ( 2 ) (2) ( 2 )
f ( 1 ) = α f ( 2 n ) = 2 f ( n ) + β ( n ⩾ 1 ) f ( 2 n + 1 ) = 2 f ( n ) + γ ( n ⩾ 1 )
\begin{equation}
\begin{array}{rll}
f(1) & = \alpha & \\
f(2n) & = 2f(n) + \beta & (n \geqslant 1) \\
f(2n + 1) & = 2f(n) + \gamma & (n \geqslant 1) \\
\end{array}
\end{equation}
f ( 1 ) f ( 2 n ) f ( 2 n + 1 ) = α = 2 f ( n ) + β = 2 f ( n ) + γ ( n ⩾ 1 ) ( n ⩾ 1 )
列举已知解
我们从 f ( 1 ) = α f(1) = \alpha f ( 1 ) = α f ( n ) f(n) f ( n )
观察与推测
观察发现,α \alpha α n n n 2 2 2 β \beta β 0 0 0 γ \gamma γ 0 0 0 f ( n ) f(n) f ( n )
f ( n ) = A ( n ) α + B ( n ) β + C ( n ) γ
\begin{equation}
f(n) = A(n)\alpha + B(n)\beta + C(n)\gamma
\end{equation}
f ( n ) = A ( n ) α + B ( n ) β + C ( n ) γ
同样,我们尝试观察规律,可以得到以下等式:
A ( n ) = 2 m B ( n ) = 2 m − 1 − l C ( n ) = l
\begin{equation}
\begin{array}{rl}
A(n) & = 2^{m} \\
B(n) & = 2^{m} - 1 - l \\
C(n) & = l \\
\end{array}
\end{equation}
A ( n ) B ( n ) C ( n ) = 2 m = 2 m − 1 − l = l
现在我们对 m m m ( α , β , γ ) = ( 1 , 0 , 0 ) (\alpha, \beta, \gamma) = (1, 0, 0) ( α , β , γ ) = ( 1 , 0 , 0 )
f ( n ) = A ( n )
\begin{equation}
f(n) = A(n)
\end{equation}
f ( n ) = A ( n )
那么递归式 ( 3 ) (3) ( 3 )
f ( 1 ) = A ( n ) = 1 f ( 2 n ) = A ( 2 n ) = 2 A ( n ) f ( 2 n + 1 ) = A ( 2 n + 1 ) = 2 A ( n )
\begin{equation}
\begin{array}{rrl}
f(1) = & A(n) & = 1 \\
f(2n) = & A(2n) & = 2A(n) \\
f(2n + 1) = & A(2n + 1) & = 2A(n)
\end{array}
\end{equation}
f ( 1 ) = f ( 2 n ) = f ( 2 n + 1 ) = A ( n ) A ( 2 n ) A ( 2 n + 1 ) = 1 = 2 A ( n ) = 2 A ( n )
∵ n = 2 m + l \because n = 2^{m} + l ∵ n = 2 m + l ∴ \therefore ∴ m = 0 m = 0 m = 0 A ( 2 0 + l ) = A ( 1 + l ) A(2^{0} + l) = A(1 + l) A ( 2 0 + l ) = A ( 1 + l ) ∵ 0 ⩽ l < 2 m \because 0 \leqslant l < 2^{m} ∵ 0 ⩽ l < 2 m l = 0 l = 0 l = 0 ∴ A ( 1 ) = 1 \therefore A(1) = 1 ∴ A ( 1 ) = 1
当 m > 0 m > 0 m > 0 2 m + l = 2 n 2^{m} + l = 2n 2 m + l = 2 n
A ( 2 m + l ) = 2 A ( n ) = 2 A ( 2 m − 1 + l / 2 ) = 2 × 2 m − 1 = 2 m
\begin{array}{ll}
A(2^{m} + l) & = 2A(n) \\
& = 2A(2^{m - 1} + l / 2) \\
& = 2 \times 2^{m - 1} \\
& = 2^{m}
\end{array}
A ( 2 m + l ) = 2 A ( n ) = 2 A ( 2 m − 1 + l /2 ) = 2 × 2 m − 1 = 2 m 当 m > 0 m > 0 m > 0 2 m + l = 2 n + 1 2^{m} + l = 2n + 1 2 m + l = 2 n + 1
A ( 2 m + l ) = 2 A ( n ) = 2 A ( 2 m − 1 + ( l − 1 ) / 2 ) = 2 × 2 m − 1 = 2 m
\begin{array}{ll}
A(2^{m} + l) & = 2A(n) \\
& = 2A(2^{m - 1} + (l - 1) / 2) \\
& = 2 \times 2^{m - 1} \\
& = 2^{m}
\end{array}
A ( 2 m + l ) = 2 A ( n ) = 2 A ( 2 m − 1 + ( l − 1 ) /2 ) = 2 × 2 m − 1 = 2 m 综上所述,A ( n ) = 2 m A(n) = 2^{m} A ( n ) = 2 m
因而,我们可以得到最终的解,其中 m ⩾ 0 m \geqslant 0 m ⩾ 0 0 ⩽ l < 2 m 0 \leqslant l < 2^{m} 0 ⩽ l < 2 m
f ( n ) = A ( n ) α + B ( n ) β + C ( n ) γ = f ( 2 m + l ) = 2 m α + ( 2 m − 1 − l ) β + l γ = 2 m ( α + β ) − ( l + 1 ) β + l γ
\begin{equation}
\begin{array}{lrl}
f(n) & & = A(n)\alpha + B(n)\beta + C(n)\gamma \\
& = f(2^{m} + l) & = 2^{m}\alpha + (2^{m} - 1 - l)\beta + l\gamma \\
& & = 2^{m}(\alpha + \beta) - (l + 1)\beta + l\gamma
\end{array}
\end{equation}
f ( n ) = f ( 2 m + l ) = A ( n ) α + B ( n ) β + C ( n ) γ = 2 m α + ( 2 m − 1 − l ) β + l γ = 2 m ( α + β ) − ( l + 1 ) β + l γ
回顾下:(1)我们计算出前 N 个递归式的值,列出表格;(2)观察表格的数据,尝试找些规律;(3)用这些规律把递归式改写成 closed form(封闭形式);(4)用归纳法等证明 closed form。
巧妙的求解方法:Repertoire Method(取值法)
这里的“取值法”中文翻译采用的是《算法分析导论》中文版,因为比较直观地表达了这种方法的核心,而《具体数学》中文版对应的翻译则是“成套方法”。
《 具体数学 》介绍了另一种求解递归式 ( 4 ) (4) ( 4 )
This approach illustrates a surprisingly useful repertoire method for solving recurrences. First we find settings of general parameters for which we know the solution; this gives us a repertoire of special cases that we can solve. Then we obtain the general case by combining the special cases. We need as many independent special solutions as there are independent parameters…
Concrete Mathematics, 2nd Edition
这个描述比较抽象,在后文将结合例子对上述描述进行解释,我们先按照原书以递归式 ( 3 ) (3) ( 3 ) f ( n ) = 1 f(n) = 1 f ( n ) = 1 f ( n ) = n f(n) = n f ( n ) = n
当 f ( n ) = 1 f(n) = 1 f ( n ) = 1
f ( 1 ) = α = 1 f ( 2 n ) = 2 f ( n ) + β = 2 × 1 + β = 1 f ( 2 n + 1 ) = 2 f ( n ) + γ = 2 × 1 + γ = 1
\begin{array}{ll}
f(1) & = \alpha = 1 \\
f(2n) & = 2f(n) + \beta \\
& = 2 \times 1 + \beta \\
& = 1 \\
f(2n + 1) & = 2f(n) + \gamma \\
& = 2 \times 1 + \gamma \\
& = 1
\end{array}
f ( 1 ) f ( 2 n ) f ( 2 n + 1 ) = α = 1 = 2 f ( n ) + β = 2 × 1 + β = 1 = 2 f ( n ) + γ = 2 × 1 + γ = 1 解得 α = 1 , β = − 1 , γ = − 1 \alpha = 1, \beta = -1, \gamma = -1 α = 1 , β = − 1 , γ = − 1
代入式子 ( 4 ) (4) ( 4 ) f ( n ) = A ( n ) − B ( n ) − C ( n ) = 1 f(n) = A(n) - B(n) - C(n) = 1 f ( n ) = A ( n ) − B ( n ) − C ( n ) = 1
当 f ( n ) = n f(n) = n f ( n ) = n
f ( 1 ) = α = 1 f ( 2 n ) = 2 f ( n ) + β = 2 × n + β = 2 n f ( 2 n + 1 ) = 2 f ( n ) + g a m m a = 2 × n + g a m m a = 2 n + 1
\begin{array}{ll}
f(1) & = \alpha = 1 \\
f(2n) & = 2f(n) + \beta \\
& = 2 \times n + \beta \\
& = 2n \
f(2n + 1) & = 2f(n) + gamma \\
& = 2 \times n + gamma \\
& = 2n + 1
\end{array}
f ( 1 ) f ( 2 n ) = α = 1 = 2 f ( n ) + β = 2 × n + β = 2 n f ( 2 n + 1 ) = 2 × n + g amma = 2 n + 1 = 2 f ( n ) + g amma 解得 α = 1 , β = 0 , γ = 1 \alpha = 1, \beta = 0, \gamma = 1 α = 1 , β = 0 , γ = 1
代入式子 ( 4 ) (4) ( 4 ) f ( n ) = A ( n ) + C ( n ) = n f(n) = A(n) + C(n) = n f ( n ) = A ( n ) + C ( n ) = n
另外,由归纳假设可证得,A ( n ) = 2 m A(n) = 2^{m} A ( n ) = 2 m n = 2 m + l n = 2^{m} + l n = 2 m + l 0 ⩽ l < 2 m 0 \leqslant l < 2^{m} 0 ⩽ l < 2 m
A ( n ) = 2 m A ( n ) − B ( n ) − C ( n ) = 1 A ( n ) + C ( n ) = n
\begin{array}{rl}
A(n) & = 2^{m} \\
A(n) - B(n) - C(n) & = 1 \\
A(n) + C(n) & = n \\
\end{array}
A ( n ) A ( n ) − B ( n ) − C ( n ) A ( n ) + C ( n ) = 2 m = 1 = n
现在可以解得:
A ( n ) = 2 m C ( n ) = n − A ( n ) = n − 2 m = l B ( n ) = 2 m − 1 − l
\begin{array}{rlll}
A(n) & = 2^{m} & & \\
C(n) & = n - A(n) & = n - 2^{m} & = l \\
B(n) & = 2^{m} - 1 - l & &
\end{array}
A ( n ) C ( n ) B ( n ) = 2 m = n − A ( n ) = 2 m − 1 − l = n − 2 m = l
最后我们得到了与式子 ( 8 ) (8) ( 8 ) ( 8 ) (8) ( 8 ) ( 1 ) (1) ( 1 )
由递归式 ( 1 ) (1) ( 1 ) α = 1 , β = − 1 , γ = 1 \alpha = 1, \beta = -1, \gamma = 1 α = 1 , β = − 1 , γ = 1
代入式子 ( 8 ) (8) ( 8 )
f ( n ) = f ( 2 m + l ) = 2 m ( 1 + ( − 1 ) ) − ( l + 1 ) × ( − 1 ) + l × 1 = 2 l + 1
\begin{array}{rlll}
f(n) & = f(2^{m} + l) \\
& = 2^{m}(1 + (-1)) - (l + 1) \times (-1) + l \times 1 \\
& = 2l + 1
\end{array}
f ( n ) = f ( 2 m + l ) = 2 m ( 1 + ( − 1 )) − ( l + 1 ) × ( − 1 ) + l × 1 = 2 l + 1 回顾下,在这个求解过程中,(1)我们取 f ( n ) = 1 f(n) = 1 f ( n ) = 1 f ( n ) = n f(n) = n f ( n ) = n ( 3 ) (3) ( 3 ) α \alpha α β \beta β γ \gamma γ ( 4 ) (4) ( 4 ) A ( n ) A(n) A ( n ) B ( n ) B(n) B ( n ) C ( n ) C(n) C ( n )
…the so-called repertoire method, where we use known functions to find a family of solutions similar to the one sought, which can be combined to give the answers. This method primarily applies to linear recurrences…
An Introduction to The Analysis of Algorithms, 2nd Edition
到目前为止,我们已经了解到,递归式的解可以由一组线性函数组合而成,因而有:
a n = A 1 ( n ) ⋅ α 1 + A 2 ( n ) ⋅ α 2 + ⋯ + A k ( n ) ⋅ α k = ∑ i = 1 k A i ( n ) ⋅ α i
\begin{array}{rl}
a_{n} & = A_{1}(n)·\alpha_{1} + A_{2}(n)·\alpha_{2} + \cdots + A_{k}(n)·\alpha_{k} \\
& =\sum_{i=1}^{k}A_{i}(n)·\alpha_{i}
\end{array}
a n = A 1 ( n ) ⋅ α 1 + A 2 ( n ) ⋅ α 2 + ⋯ + A k ( n ) ⋅ α k = ∑ i = 1 k A i ( n ) ⋅ α i
可惜《 具体数学 》轻描淡写地介绍了这种方法,看得云里雾里。在另外一本书籍《 算法分析导论(第二版) 》找到了进一步的说明,作者列举了 Repertoire Method 的步骤:
Relax the recurrence by adding an extra functional term
Substitute known functions into the recurrence to derive identities similar to the recurrence
Take linear combinations of such identities to derive an equation identical to the recurrence
说得还是挺抽象的,我们需要更多的例子来进一步理解这种技巧。不幸的是,由于《 算法分析导论 》的作者在“勘误列表”指出,书中给出的例子“is bad; needs to be replaced”,我只好借用发表在 StackExchange 关于 Repertoire Method 问题的回答 。
StackExchange 回答者给出以下例子(本文在求解过程中做了稍微的修改,以符合上文的描述):
a n = a n − 1 + 2 n 2 + 7 ( n > 0 且 a 0 = 7 )
\begin{array}{ll}
a_{n} = a_{n-1} + 2n^{2} + 7 & (n > 0 且 a_{0} = 7)
\end{array}
a n = a n − 1 + 2 n 2 + 7 ( n > 0 且 a 0 = 7 )
首先,泛化这个递归式。令 f ( n ) = 2 n 2 + 7 f(n) = 2n^{2} + 7 f ( n ) = 2 n 2 + 7 a n = a n − 1 + f ( n ) a_{n} = a_{n-1} + f(n) a n = a n − 1 + f ( n ) f ( n ) = a n − a n − 1 = 2 n 2 + 7 f(n) = a_{n} - a_{n-1} = 2n^{2} + 7 f ( n ) = a n − a n − 1 = 2 n 2 + 7 a n a_{n} a n
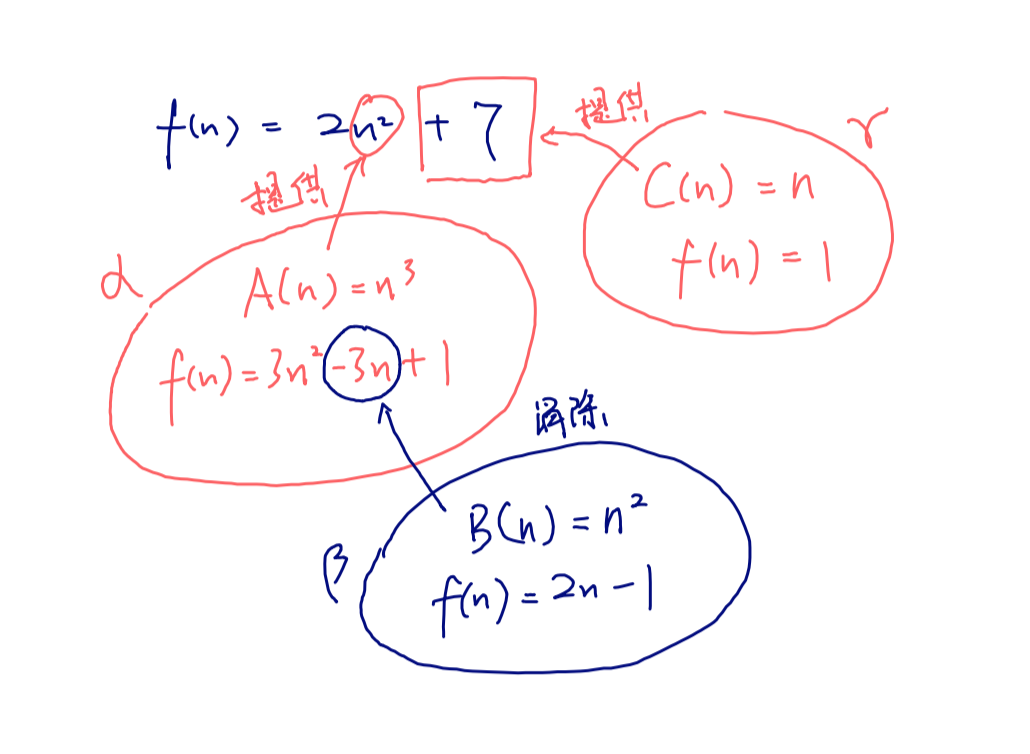
观察 f ( n ) = 2 n 2 + 7 f(n) = 2n^{2}+7 f ( n ) = 2 n 2 + 7 n 2 n^2 n 2 7 7 7 a n = n 3 a_{n}=n^{3} a n = n 3 f ( n ) = 3 n 2 − 3 n + 1 f(n) = 3n^{2}-3n+1 f ( n ) = 3 n 2 − 3 n + 1 n 2 n^{2} n 2 n n n f ( n ) f(n) f ( n ) a n = n 2 a_{n}=n^{2} a n = n 2 2 n − 1 2n-1 2 n − 1 n n n β \beta β n n n a n = 1 a_{n}=1 a n = 1 f ( n ) = 1 f(n)=1 f ( n ) = 1 1 1 1
确定参数过程的示意图
这样我们找到了一套特殊函数( a repertoire of special cases that we can solve ):A ( n ) = n 3 A(n) = n^3 A ( n ) = n 3 B ( n ) = n 2 B(n) = n^{2} B ( n ) = n 2 C ( n ) = n C(n) = n C ( n ) = n
现在,我们组合这几个函数( combining the special cases ),令 a n = A ( n ) α + B ( n ) β + C ( n ) γ a_{n} = A(n)\alpha + B(n)\beta + C(n)\gamma a n = A ( n ) α + B ( n ) β + C ( n ) γ
a n = α n 3 + β n 2 + γ n
\begin{equation}
a_{n} = \alpha n^3 + \beta n^{2} + \gamma n
\end{equation}
a n = α n 3 + β n 2 + γn
现在我们开始解这三个参数 α \alpha α β \beta β γ \gamma γ
对 f ( n ) = 2 n 2 + 7 f(n) = 2n^{2}+7 f ( n ) = 2 n 2 + 7 find settings of general parameters for which we know the solution ):
当 f ( n ) = 1 f(n)=1 f ( n ) = 1 a n = n a_{n}=n a n = n
当 f ( n ) = 2 n − 1 f(n)=2n-1 f ( n ) = 2 n − 1 a n = n 2 a_{n}=n^2 a n = n 2
当 f ( n ) = 3 n 2 − 3 n + 1 f(n)=3n^{2}-3n+1 f ( n ) = 3 n 2 − 3 n + 1 a n = n 3 a_{n}=n^3 a n = n 3
则
f ( n ) = 2 n 2 + 7 = α ( 3 n 2 − 3 n + 1 ) + β ( 2 n − 1 ) + γ ( 1 ) = 3 α n 2 + ( − 3 α + 2 β ) n + ( α − β + γ )
\begin{array}{rl}
f(n) & = 2n^{2}+7 \\
& = \alpha (3n^{2}-3n+1) + \beta (2n-1) + \gamma (1) \\
& = 3 \alpha n^{2} + (-3 \alpha + 2 \beta) n + (\alpha - \beta + \gamma) \\
\end{array}
f ( n ) = 2 n 2 + 7 = α ( 3 n 2 − 3 n + 1 ) + β ( 2 n − 1 ) + γ ( 1 ) = 3 α n 2 + ( − 3 α + 2 β ) n + ( α − β + γ ) 对应的系数方程,有
{ 3 α = 2 − 3 α + 2 β = 0 α − β + γ = 7
\begin{cases}
3\alpha = 2 \\
-3\alpha + 2\beta = 0 \\
\alpha - \beta + \gamma = 7
\end{cases}
⎩ ⎨ ⎧ 3 α = 2 − 3 α + 2 β = 0 α − β + γ = 7 解得:
α = 2 3 , β = 1 , γ = 22 3
\alpha = \frac{2}{3}, \beta = 1, \gamma = \frac{22}{3}
α = 3 2 , β = 1 , γ = 3 22 代入式子 ( 9 ) (9) ( 9 )
a n = 2 3 n 3 + n 2 + 22 3 n = 1 3 n ( 2 n 2 + 3 n + 22 )
\begin{equation}
\begin{array}{ll}
a_{n} & = \frac{2}{3} n^3 + n^{2} + \frac{22}{3} n \\
& = \frac{1}{3} n (2 n^2 + 3 n + 22)
\end{array}
\end{equation}
a n = 3 2 n 3 + n 2 + 3 22 n = 3 1 n ( 2 n 2 + 3 n + 22 ) 最后,我们检验式子 ( 10 ) (10) ( 10 ) a 0 = 0 a_{0}=0 a 0 = 0 a 0 = 7 a_{0}=7 a 0 = 7 ( 10 ) (10) ( 10 ) 7 7 7
a n = 1 3 n ( 2 n 2 + 3 n + 22 ) + 7
a_{n} = \frac{1}{3} n (2 n^2 + 3 n + 22) + 7
a n = 3 1 n ( 2 n 2 + 3 n + 22 ) + 7
回顾下,在这个求解过程中,(1)我们尽可能取多个 a n a_{n} a n f ( n ) f(n) f ( n ) f ( n ) f(n) f ( n ) a n a_{n} a n a n a_{n} a n a n a_{n} a n f ( n ) f(n) f ( n ) f ( n ) f(n) f ( n ) a n a_{n} a n
按照这个过程,借用一篇 博文 的例子再做说明:
a n = a n − 1 + n 3 ( n > 0 且 a 0 = 0 )
\begin{array}{ll}
a_{n} = a_{n-1} + n^3 & (n > 0 且 a_{0} = 0)
\end{array}
a n = a n − 1 + n 3 ( n > 0 且 a 0 = 0 )
首先,令 f ( n ) = n 3 f(n) = n^3 f ( n ) = n 3 f ( n ) = a n − a n − 1 f(n) = a_{n} - a_{n-1} f ( n ) = a n − a n − 1 a n a_{n} a n f ( n ) = a n − a n − 1 f(n) = a_{n} - a_{n-1} f ( n ) = a n − a n − 1
观察 f ( n ) = n 3 f(n)=n^{3} f ( n ) = n 3 n 3 n^{3} n 3 a n = n 4 a_{n}=n^4 a n = n 4 n 3 n^{3} n 3 n 2 n^{2} n 2 n n n 1 1 1 a n = n 3 a_{n}=n^3 a n = n 3 a n = n 2 a_{n}=n^2 a n = n 2 a n = n a_{n}=n a n = n
把上述候选的 a n a_{n} a n A ( n ) A(n) A ( n ) B ( n ) B(n) B ( n ) C ( n ) C(n) C ( n ) D ( n ) D(n) D ( n ) a n = A ( n ) α + B ( n ) β + C ( n ) γ + D ( n ) λ + c a_{n} = A(n) \alpha + B(n) \beta + C(n) \gamma + D(n) \lambda + c a n = A ( n ) α + B ( n ) β + C ( n ) γ + D ( n ) λ + c c c c
a n = α n 4 + β n 3 + γ n 2 + λ n + c
\begin{equation}
a_{n} = \alpha n^4 + \beta n^{3} + \gamma n^{2} + \lambda n + c
\end{equation}
a n = α n 4 + β n 3 + γ n 2 + λn + c
现在我们开始求解对应的四个参数 α \alpha α β \beta β γ \gamma γ λ \lambda λ
对 f ( n ) = n 3 f(n) = n^{3} f ( n ) = n 3
当 f ( n ) = 1 f(n)=1 f ( n ) = 1 a n = n a_{n}=n a n = n
当 f ( n ) = 2 n − 1 f(n)=2n-1 f ( n ) = 2 n − 1 a n = n 2 a_{n}=n^2 a n = n 2
当 f ( n ) = 3 n 2 − 3 n + 1 f(n)=3n^{2}-3n+1 f ( n ) = 3 n 2 − 3 n + 1 a n = n 3 a_{n}=n^3 a n = n 3
当 f ( n ) = 4 n 3 − 6 n 2 + 4 n − 1 f(n)=4n^{3}-6n^{2}+4n-1 f ( n ) = 4 n 3 − 6 n 2 + 4 n − 1 a n = n 3 a_{n}=n^3 a n = n 3
则
f ( n ) = n 3 = α ( 4 n 3 − 6 n 2 + 4 n − 1 ) + β ( 3 n 2 − 3 n + 1 ) + γ ( 2 n − 1 ) + λ ( 1 ) = 4 α n 3 + ( − 6 α + 3 β ) n 2 + ( 4 α − 3 β + 2 λ ) n + ( − α + β − γ + λ )
\begin{array}{rl}
f(n) & = n^{3} \\
& = \alpha (4n^{3}-6n^{2}+4n-1) + \beta (3n^{2}-3n+1) + \gamma (2n-1) + \lambda (1) \\
& = 4 \alpha n^{3} + (-6 \alpha + 3 \beta) n^{2} + (4 \alpha - 3 \beta + 2 \lambda) n + (- \alpha + \beta - \gamma + \lambda) \\
\end{array}
f ( n ) = n 3 = α ( 4 n 3 − 6 n 2 + 4 n − 1 ) + β ( 3 n 2 − 3 n + 1 ) + γ ( 2 n − 1 ) + λ ( 1 ) = 4 α n 3 + ( − 6 α + 3 β ) n 2 + ( 4 α − 3 β + 2 λ ) n + ( − α + β − γ + λ ) 对应的系数方程,有
{ 4 α = 1 − 6 α + 3 β = 0 4 α − 3 β + 2 λ = 0 − α + β − γ + λ = 0
\begin{cases}
4 \alpha = 1 \\
-6 \alpha + 3 \beta = 0 \\
4 \alpha - 3 \beta + 2 \lambda = 0 \\
- \alpha + \beta - \gamma + \lambda = 0
\end{cases}
⎩ ⎨ ⎧ 4 α = 1 − 6 α + 3 β = 0 4 α − 3 β + 2 λ = 0 − α + β − γ + λ = 0 解得:
α = γ = 1 4 , β = 1 2 , λ = − 1 2
\alpha = \gamma = \frac{1}{4}, \beta = \frac{1}{2}, \lambda = -\frac{1}{2}
α = γ = 4 1 , β = 2 1 , λ = − 2 1 代入式子 ( 11 ) (11) ( 11 )
a n = 1 4 n 4 + 1 2 n 3 + 1 4 n 2 − 1 2 + c = 1 4 n 2 ( n 2 + 2 n + 1 ) − 1 2 + c = 1 4 n 2 ( n + 1 ) 2 − 1 2 + c
\begin{array}{rl}
a_{n} & = \frac{1}{4} n^{4} + \frac{1}{2} n^{3} + \frac{1}{4} n^{2} - \frac{1}{2} + c \\
& = \frac{1}{4} n^{2} (n^{2} + 2 n + 1) - \frac{1}{2} + c \\
& = \frac{1}{4} n^{2} (n + 1)^{2} - \frac{1}{2} + c
\end{array} \\
a n = 4 1 n 4 + 2 1 n 3 + 4 1 n 2 − 2 1 + c = 4 1 n 2 ( n 2 + 2 n + 1 ) − 2 1 + c = 4 1 n 2 ( n + 1 ) 2 − 2 1 + c ∵ a 0 = 0 ∴ c = 1 2 \because a_{0} = 0 \therefore c = \frac{1}{2} ∵ a 0 = 0 ∴ c = 2 1
a n = 1 4 n 2 ( n + 1 ) 2
a_{n} = \frac{1}{4} n^{2} (n + 1)^{2}
a n = 4 1 n 2 ( n + 1 ) 2 总结
《 具体数学 》作者先以“猜想与归纳”(Guess and Induction)的方法求解递归式,步骤如下:
计算前 N 个递归的结果,列成表格
观察表格,找出规律
整合规律,得到 closed form(封闭形式)即递归式的解
用归纳法等数学方法证明结果成立
接着,作者尝试了另一种方法,把递归式的解定义为一组线性函数及一组参数构成:a n = ∑ i = 1 k A i ( n ) ⋅ α i a_{n}=\sum_{i=1}^{k}A_{i}(n)·\alpha_{i} a n = ∑ i = 1 k A i ( n ) ⋅ α i
令递归式的解为多个线性函数构成,设 a n = f ( n ) = A ( n ) α + B ( n ) β + C ( n ) γ a_{n} = f(n) = A(n) \alpha + B(n) \beta + C(n) \gamma a n = f ( n ) = A ( n ) α + B ( n ) β + C ( n ) γ
取多个 a n a_{n} a n a n = 1 a_{n}=1 a n = 1 a n = n a_{n}=n a n = n a n = n 2 a_{n}=n^2 a n = n 2
分别代入原递归式,列出多组参数方程组,解得多组参数的值
每组参数的值代入 f ( n ) f(n) f ( n )
把解得的线性函数与原递归式的参数代入 f ( n ) f(n) f ( n )
最后,按照《 算法分析导论 》作者的思路,同样以 Repertoire Method 求解,不过步骤稍有不同:
令递归式的解为多个线性函数构成,设 a n = ∑ i = 1 k A i ( n ) ⋅ α i + c a_{n} = \sum_{i=1}^{k}A_{i}(n)·\alpha_{i} + c a n = ∑ i = 1 k A i ( n ) ⋅ α i + c
把原递归式转换成 a n = g ( a n − 1 , a n − 2 , . . . , a 0 ) + f ( n ) a_{n} = g(a_{n-1}, a_{n-2}, ..., a_{0}) + f(n) a n = g ( a n − 1 , a n − 2 , ... , a 0 ) + f ( n )
取多个 a n a_{n} a n a n = 1 a_{n}=1 a n = 1 a n = n a_{n}=n a n = n a n = n 2 a_{n}=n^2 a n = n 2 f ′ ( n ) = a n − g ( a n − 1 , a n − 2 , . . . , a 0 ) f'(n) = a_{n} - g(a_{n-1}, a_{n-2}, ..., a_{0}) f ′ ( n ) = a n − g ( a n − 1 , a n − 2 , ... , a 0 )
观察原 f ( n ) f(n) f ( n ) a n a_{n} a n A i ( n ) A_{i}(n) A i ( n ) k k k α i \alpha_{i} α i a n a_{n} a n f ′ ( n ) f'(n) f ′ ( n ) f α i ′ ( n ) f'_{\alpha_{i}}(n) f α i ′ ( n )
建立等式:∑ i = 1 k α i ⋅ f α i ′ ( n ) = f ( n ) \sum_{i=1}^{k} \alpha_{i} · f'_{\alpha_{i}}(n) = f(n) ∑ i = 1 k α i ⋅ f α i ′ ( n ) = f ( n )
把参数值代入 a n = ∑ i = 1 k A i ( n ) ⋅ α i + c a_{n} = \sum_{i=1}^{k}A_{i}(n)·\alpha_{i} + c a n = ∑ i = 1 k A i ( n ) ⋅ α i + c c c c
后记
《 具体数学 》第一章引入了 Repertoire Method 来求解递归式,据说在后续章节中频繁运用,那么熟悉这种技巧及其应用,有助于理解后续的章节,所以花了比较多的时间学习这种技巧,不过依然还有些问题未得到解决,比如:
Repertoire Method 的原理是什么?为什么递归式的解可以由多个线性函数组合?
如何更加合理地确定参数的个数?为什么《 具体数学 》只用了三个参数就足够了?(事实上本文的例子都可以默认用三个参数来解)
…
在《 算法分析导论 》提到了这种技巧的实际应用:求解快速排序的的递归式,具体求解过程可以 参考 StackExchange 的回答 。其他更多的例题可通过下面的“参考资料”获得。